Coefficient Of Variance Excel

Understanding Coefficient of Variance in Excel

The Coefficient of Variance (CV) is a statistical measure that calculates the relative variability of a dataset. It is defined as the ratio of the standard deviation to the mean, often expressed as a percentage. In Excel, calculating the Coefficient of Variance can be useful for comparing the variability of different datasets. This post will guide you through the process of calculating the Coefficient of Variance in Excel and provide examples of its application.
Calculating Coefficient of Variance in Excel

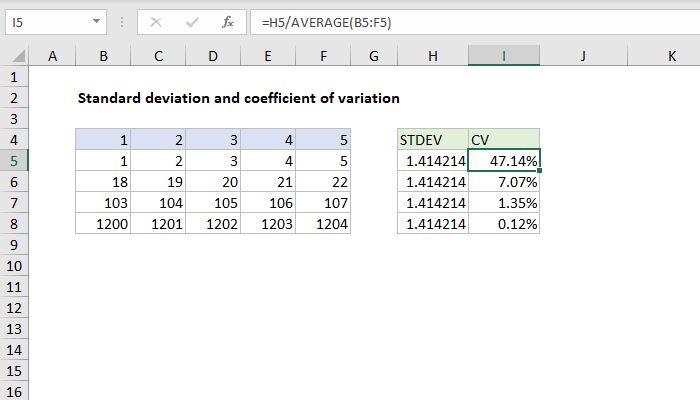
To calculate the Coefficient of Variance in Excel, you can use the following formula: CV = (Standard Deviation / Mean) * 100 Where: - Standard Deviation is calculated using the STDEV function in Excel. - Mean is calculated using the AVERAGE function in Excel. Here’s a step-by-step guide to calculating the Coefficient of Variance in Excel: - First, calculate the mean of your dataset using the formula: =AVERAGE(range) - Next, calculate the standard deviation of your dataset using the formula: =STDEV(range) - Then, calculate the Coefficient of Variance using the formula: =(STDEV(range) / AVERAGE(range)) * 100
Example of Coefficient of Variance Calculation

Suppose we have a dataset of exam scores: 80, 70, 90, 85, 75 To calculate the Coefficient of Variance, we first calculate the mean: =AVERAGE(80, 70, 90, 85, 75) = 80 Then, we calculate the standard deviation: =STDEV(80, 70, 90, 85, 75) = 7.071 Finally, we calculate the Coefficient of Variance: =(7.071 / 80) * 100 = 8.839%
Interpreting Coefficient of Variance

The Coefficient of Variance is a unitless measure, making it useful for comparing the variability of datasets with different units. A low Coefficient of Variance indicates that the data points are close to the mean, while a high Coefficient of Variance indicates that the data points are spread out. Here are some general guidelines for interpreting the Coefficient of Variance: * CV < 10%: Low variability * 10% < CV < 20%: Moderate variability * CV > 20%: High variability
Applications of Coefficient of Variance

The Coefficient of Variance has several applications in finance, engineering, and quality control. Some examples include: * Finance: Calculating the Coefficient of Variance of stock prices or returns can help investors assess the risk of an investment. * Engineering: Calculating the Coefficient of Variance of manufacturing process data can help engineers assess the consistency of the process. * Quality Control: Calculating the Coefficient of Variance of quality control data can help manufacturers assess the consistency of their products.
Using Coefficient of Variance in Data Analysis

The Coefficient of Variance can be used in conjunction with other statistical measures, such as the mean and standard deviation, to gain a deeper understanding of a dataset. Here are some tips for using the Coefficient of Variance in data analysis: * Use the Coefficient of Variance to compare the variability of different datasets. * Use the Coefficient of Variance to identify outliers in a dataset. * Use the Coefficient of Variance to assess the consistency of a manufacturing process or quality control data.
📝 Note: The Coefficient of Variance is sensitive to extreme values, so it's essential to check for outliers before calculating the Coefficient of Variance.
| Dataset | Mean | Standard Deviation | Coefficient of Variance |
|---|---|---|---|
| Exam Scores | 80 | 7.071 | 8.839% |
| Stock Prices | 100 | 10 | 10% |

In summary, the Coefficient of Variance is a useful statistical measure that calculates the relative variability of a dataset. By following the steps outlined in this post, you can calculate the Coefficient of Variance in Excel and use it to gain a deeper understanding of your data. Whether you’re working in finance, engineering, or quality control, the Coefficient of Variance is an essential tool for data analysis.
To recap, the key points to take away from this post are: * The Coefficient of Variance is calculated using the formula: CV = (Standard Deviation / Mean) * 100 * The Coefficient of Variance is a unitless measure, making it useful for comparing the variability of datasets with different units * A low Coefficient of Variance indicates that the data points are close to the mean, while a high Coefficient of Variance indicates that the data points are spread out * The Coefficient of Variance has several applications in finance, engineering, and quality control
What is the Coefficient of Variance?

+
The Coefficient of Variance is a statistical measure that calculates the relative variability of a dataset. It is defined as the ratio of the standard deviation to the mean, often expressed as a percentage.
How is the Coefficient of Variance calculated?

+
The Coefficient of Variance is calculated using the formula: CV = (Standard Deviation / Mean) * 100
What are the applications of the Coefficient of Variance?
+
The Coefficient of Variance has several applications in finance, engineering, and quality control. It can be used to compare the variability of different datasets, identify outliers, and assess the consistency of a manufacturing process or quality control data.



